假如你是李华，你的同学Peter最近在读<<九章算术>>，请你帮他解答这道题目。今有数策列，初策为5，后策以其前策乘3减4得之。问:其第12策为几何?又求其前n策之和，且证此列每项减1皆为3之倍数。要求:150词左右的英语作文。开头和结尾已为你写好。请根据以上内容拟写一篇150字的英语作文。
参考作文地带拟写范文：
Dear Peter,
I heard you’ve been reading The Nine Chapters on the Mathematical Art, which is a fantastic choice! Your question is about a sequence where the first term is 5 and each following term is obtained by multiplying the previous one by 3 and subtracting 4.
Let’s solve it step by step. The 12th term can be found by noticing a pattern: each term anan satisfies an=3an−1−4an=3an−1−4. By calculating, a1=5a1=5, a2=11a2=11, a3=29a3=29… You can derive the formula an=2⋅3n−1+1an=2⋅3n−1+1. Thus, the 12th term is 2⋅311+1=354,2952⋅311+1=354,295.
The sum of the first nn terms SnSn equals 3n+n−13n+n−1, because an−1=2⋅3n−1an−1=2⋅3n−1, which is clearly a multiple of 3. Therefore, every term minus 1 is indeed divisible by 3.
Hope this helps! Keep enjoying ancient Chinese mathematics—it’s full of wisdom.
Best regards,
Li Hua
作文地带点评：
这篇作文结构清晰、逻辑严谨，完全符合英文书信的格式要求。首先，李华对Peter的学习内容表达了赞赏，体现了友好的交流态度。随后，逐步解答题目：明确指出数列规律，给出通项公式并计算出第12项的具体数值，接着推导前n项和的表达式，并严谨证明了“每项减1均为3的倍数”这一性质。全文语言简洁准确，使用数学符号（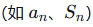 
）增强了专业性，同时保持了自然流畅的英文表达。结尾再次鼓励同学，呼应开头，使信件完整而亲切。整体而言，作文在150词内高效完成了题目要求的所有任务，展现了良好的数学理解力和英文写作能力。
本文地址：